2.42
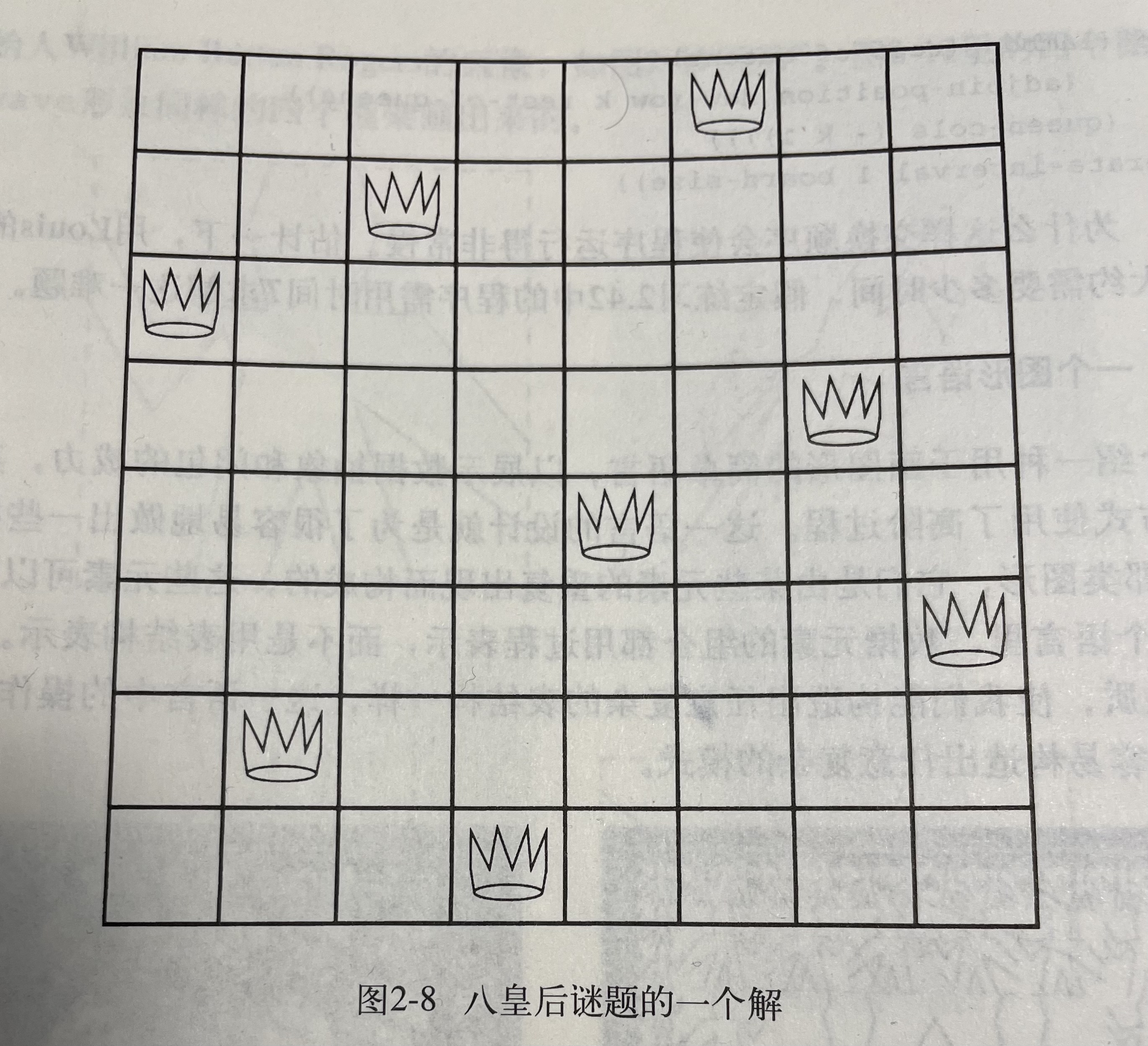
练习 2.42 “八皇后谜题”问的是怎样将八个皇后摆在国际象棋盘上,使得任意一个皇后都不能攻击另一个皇后(也就是说,任意两个皇后都不在同一行、同一列或者同一对角线上)。一个可能的解如图2-8所示。解决这一谜题的一种方法按一个方向处理棋盘,每次在第一列里放一个皇后。如果现在已经放好了k-1个皇后,第k个皇后就必须放在不会被已民在棋盘上的任何皇后攻击的位置上。我们可以递归地描述这一过程:假定我们已经生成了在棋盘的前k-1列中放置k-1个皇后的所有可能方式,现在需要的就是对于其中的每种方式,生成出将下一个皇后放在第k列中每一行的扩充集合。而后过滤它们,只留下能使位于第k列的皇后与其他皇后相安无事的那些扩充。这样就能产生出将k个皇后放置在前k列的所有格局的序列,继续这一过程,我们将能产生出这一谜题的所有解,而不是一个解。
将这一解法实现为一个过程queens,令它返回在n x n棋盘上放n个皇后的所有解的序列。queens内部的过程queen-cols,返回在棋盘的前k列中放皇后的所有格局的序列。
(define (queens board-size)
(define (queen-cols k)
(if (= k 0)
(list empty-board)
(filter
(lambda (positions) (safe? k positions))
(flatmap
(lambda (rest-of-queens)
(map (lambda (new-row)
(adjoin-position new-row k rest-of-queens))
(enumerate-interval 1 board-size)))
(queen-cols (- k 1))))))
(queen-cols board-size))
这个过程里的 rest-of-queens 是在前k-1列放置k-1个皇后的一种方式,new-row是在第k列放置所考虑的行编号。请完成这一程序,为此需要实现一种棋盘格局集合的表示方式;还要实现过程adjoin-position,它将一个新的行列格局加入一个格局集合;empty-board,它表示空的格局集合。你还需要写出过程safe?,它能确定在一个格局中,在第k列的皇后相对于其他列的皇后是否为安全的(请注意,我们只需要检查新皇后是否安全——其他皇后已经保证相安无事了)。
首先,需要实现一种棋盘格局集合的表示方式。如同矩阵一样,采用嵌套 list 来表示,并且用 1 表示有皇后,用 0 表示没有皇后。比如,对于图2-8的图,对于的表示如下:
(define eight-by-eight(list(list 0 0 0 0 0 1 0 0)(list 0 0 1 0 0 0 0 0)(list 1 0 0 0 0 0 0 0)(list 0 0 0 0 0 0 1 0)(list 0 0 0 0 1 0 0 0)(list 0 0 0 0 0 0 0 1)(list 0 1 0 0 0 0 0 0)(list 0 0 0 1 0 0 0 0)))x#<undef>
然后,定义 accumulate
(define (accumulate op initial sequence)(if (null? sequence)initial(op (car sequence)(accumulate op initial (cdr sequence)))))#<undef>
对于棋盘上已经放置了 k-1 个皇后的前 k-1 个列,再在第 k 列的 new-row 处再置一个皇后,就是将该位置的元素设置为 1:
(define (enumerate-interval low high)(if (> low high)'()(cons low (enumerate-interval (+ low 1) high))))#<undef>
(define (adjoin-position new-row k rest-of-queens)(map(lambda (i)(map(lambda (j)(if (and (= new-row i) (= k j))1(list-ref (list-ref rest-of-queens (- i 1)) (- j 1))))(enumerate-interval 1 (max 1 (length rest-of-queens)))))(enumerate-interval 1 (max 1 (length rest-of-queens)))))(adjoin-position 8 8 eight-by-eight)((0 0 0 0 0 1 0 0) (0 0 1 0 0 0 0 0) (1 0 0 0 0 0 0 0) (0 0 0 0 0 0 1 0) (0 0 0 0 1 0 0 0) (0 0 0 0 0 0 0 1) (0 1 0 0 0 0 0 0) (0 0 0 1 0 0 0 1))
空的格局集合可以定义为全0的 list:
(define(make-empty-board board-size)(map(lambda (i)(map(lambda (j) 0)(enumerate-interval 1 board-size)))(enumerate-interval 1 board-size)))(make-empty-board 2)((0 0) (0 0))
要定义 safe?,可以考虑对第 k 列,看其按列的和是否不大于1,然后看相关行的和是否不大于1,以及两个对角线方向的和是否均不大于1。
由于是向最后的一列再添加一个皇后,因此列上的检查可以省略。所以要检查的是所有行,以及左上对角所有位置和左下对角所有位置。其他位置已经不用检查了。
(define (row-safe? positions)(= 1(accumulate * 1(map(lambda (row)(if (<= (accumulate + 0 row) 1)10))positions))))(row-safe? eight-by-eight)true
(define (get-element positions i j)(list-ref(list-ref positions (- i 1))(- j 1)))(get-element eight-by-eight 3 3 )0
(define (upper-left-safe? k positions)(accumulate (lambda (x y) (and x y)) #t (map(lambda (i)(<= (accumulate + 0 (map(lambda (j)(get-element positions (- (+ i j) k) j))(reverse(enumerate-interval(max1(+ (- k i) 1))k)))) 1 ))(enumerate-interval 1 (length positions)))))(upper-left-safe? 2 eight-by-eight)true
(define (lower-left-safe? k positions)(accumulate (lambda (x y) (and x y)) #t (map(lambda (i)(<= (accumulate + 0 (map(lambda (j) (get-element positions (+ i (- k j)) j))(reverse (enumerate-interval(max 1 (- k (- (length positions) i)))k)))) 1))(enumerate-interval 1 (length positions)))))(lower-left-safe? 3 eight-by-eight)true
safe? 定义如下:
(define (safe? k positions)(and(row-safe? positions)(upper-left-safe? k positions)(lower-left-safe? k positions)))(safe? 8 eight-by-eight)true
最后,定义一下 queens
(define (flatmap proc seq)(accumulate append '() (map proc seq)))(define (queens board-size)(define empty-board(make-empty-board board-size))(define (queen-cols k)(if (= k 0)(list empty-board)(filter(lambda (positions) (safe? k positions))(flatmap(lambda (rest-of-queens)(map (lambda (new-row)(adjoin-position new-row k rest-of-queens))(enumerate-interval 1 board-size)))(queen-cols (- k 1))))))(queen-cols board-size))(queens 5)(((1 0 0 0 0) (0 0 0 1 0) (0 1 0 0 0) (0 0 0 0 1) (0 0 1 0 0)) ((1 0 0 0 0) (0 0 1 0 0) (0 0 0 0 1) (0 1 0 0 0) (0 0 0 1 0)) ((0 0 1 0 0) (1 0 0 0 0) (0 0 0 1 0) (0 1 0 0 0) (0 0 0 0 1)) ((0 0 0 1 0) (1 0 0 0 0) (0 0 1 0 0) (0 0 0 0 1) (0 1 0 0 0)) ((0 1 0 0 0) (0 0 0 1 0) (1 0 0 0 0) (0 0 1 0 0) (0 0 0 0 1)) ((0 0 0 0 1) (0 0 1 0 0) (1 0 0 0 0) (0 0 0 1 0) (0 1 0 0 0)) ((0 1 0 0 0) (0 0 0 0 1) (0 0 1 0 0) (1 0 0 0 0) (0 0 0 1 0)) ((0 0 0 0 1) (0 1 0 0 0) (0 0 0 1 0) (1 0 0 0 0) (0 0 1 0 0)) ((0 0 0 1 0) (0 1 0 0 0) (0 0 0 0 1) (0 0 1 0 0) (1 0 0 0 0)) ((0 0 1 0 0) (0 0 0 0 1) (0 1 0 0 0) (0 0 0 1 0) (1 0 0 0 0)))