2.34

练习 2.34 对于x的某个给定值，求出一个多项式在x值，也可以形式化为一种累积。假定需要求下面多项式的值：

$$a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0$$

采用著名的Horner规则，可以构造出下面的计算：

$$(\cdots (a_nx + a_{n-1})x + \cdots + a_1) x + a_0$$

换名话说，我们可以从a_n开始，乘以x，再加上$a_{n-1}$，乘以x，如此下去，直到处理完$a_0$。请填充下面的模板，做出一个复用Horner规则求多项式值的过程。假定多项式的系数安排在一个序列里，从$a_0$直至$a_n$。

(define (horner-eval x coefficient-sequence)
    (accumulate (lambda (this-coeff higher-terms) <??>)
                0
                coefficient-sequence))

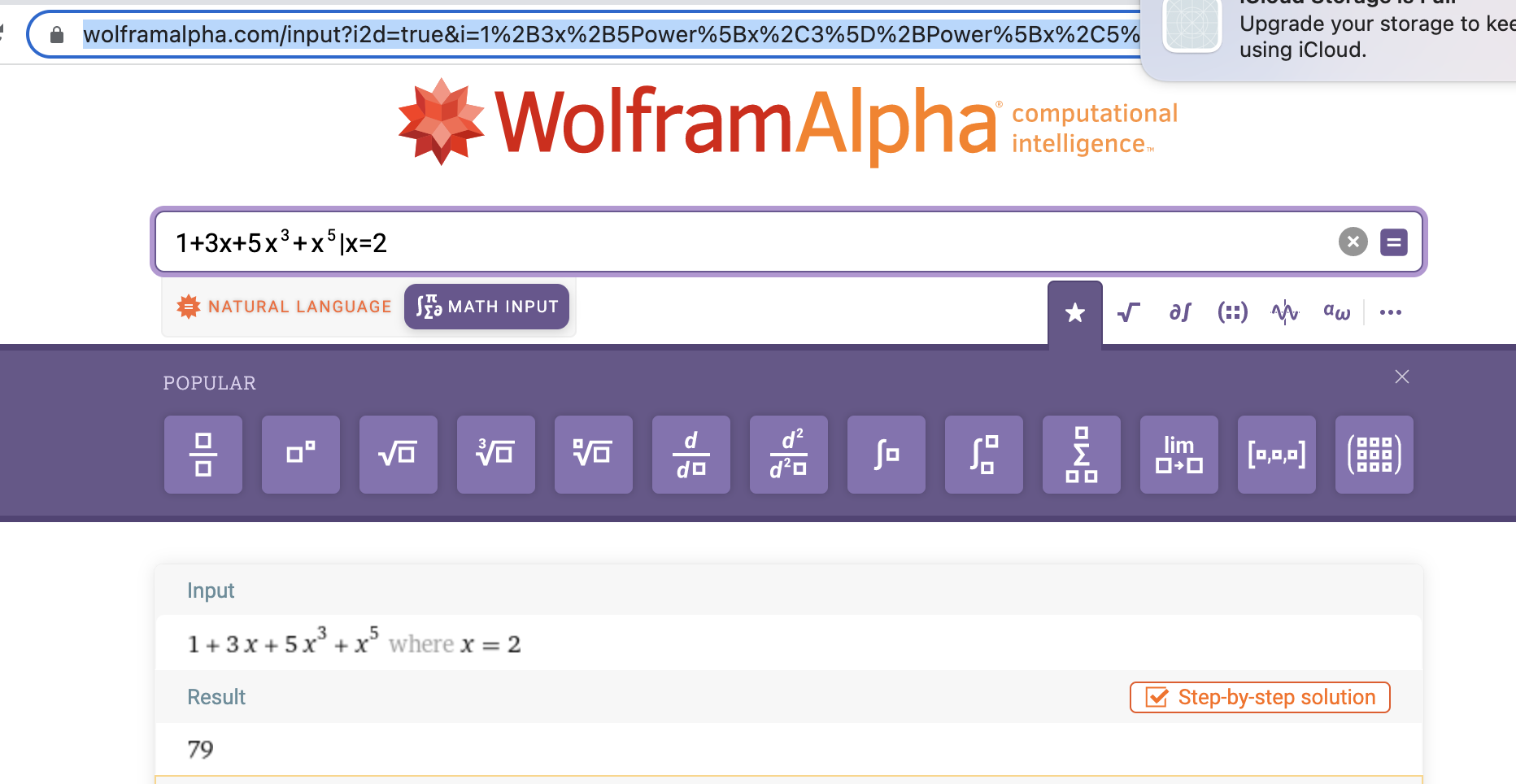
例如，为了计算$1+3x + 5x^3 + x^5$在x=2的值，你需要求值：

(horner-eval 2 (list 1 3 0 5 0 1))

首先，定义 accumulate

(define (accumulate op initial sequence)
    (if (null? sequence)
        initial
        (op (car sequence)
            (accumulate op initial (cdr sequence))) 
    )
)

(define (horner-eval x coefficient-sequence)
    (accumulate (lambda (this-coeff higher-terms) (+ this-coeff (* higher-terms x)))
                0
                coefficient-sequence))

(horner-eval 2 (list 1 3 0 5 0 1))

对比：