2.71

练习 2.71 假定我们有一棵n个符号的字母表的Huffman树，其中各符号的相对频度分别是1，2，4，…，$2^{n-1}$。请对n=5和n=10勾勒出有关的树的样子。对于这样的树（对于一般的n），编码出现最频繁的符号用多少个二进制位？最不频繁的符号呢？

先复用一下前面的代码：

(define (make-leaf-set pairs)
    (if (null? pairs)
        '()
        (let ((pair (car pairs)))
            (adjoin-set 
                (make-leaf (car pair) (cadr pair))
                (make-leaf-set (cdr pairs))
            )
        )
    )
)   


(define (adjoin-set x set)
  (cond
   ((null? set) (list x))
   ((<= (weight x) (weight (car set))) (cons x set))
   (else (cons (car set) (adjoin-set x (cdr set))))
   )
)


(define (leaf? object) (eq? (car object) 'leaf))

(define (symbol-leaf x) (cadr x))
(define (weight-leaf x) (caddr x))


(define (left-branch tree) 
    (car tree)
)

(define (right-branch tree) 
    (if (null? (cdr tree))
        '()
        (cadr tree)
    )
)

(define (encode-symbol-with-code char tree code)    
    (if (leaf? tree)
        (if (eq? (symbol-leaf tree) char)
            (list code)
            '()
        )

        (let
            (
                (left (encode-symbol-with-code char (left-branch tree) '0))
                (right (encode-symbol-with-code char (right-branch tree) '1))  
            )

            (let
                (
                    (res (append left right))
                )

                (if (null? res)
                    '()
                    (append (list code) res) 
                )
            )
        )
    )
)

(define (encode-symbol char tree)
    ; (encode-symbol-with-code char tree '0)

    (if (leaf? tree)
        (if (eq? (symbol-leaf tree) char)
            (list '0)
            '()
        )

        (let
            (
                (left-res (encode-symbol-with-code char (left-branch tree) '0))
                (right-res (encode-symbol-with-code char (right-branch tree) '1))
            )

            (append left-res right-res)
        )
    )
)


(define (decode bits tree)
    (define (decode-1 bits current-branch)
        (if (null? bits)
            '()
            (let 
                (
                    (next-branch
                        (choose-branch 
                            (car bits)
                            current-branch
                        )
                    )
                )

                (if (leaf? next-branch)
                    (cons 
                        (symbol-leaf next-branch) 
                        (decode-1 (cdr bits) tree)
                    )
                    (decode-1 (cdr bits) next-branch)
                )
            )
        )
    )

    (decode-1 bits tree)
)

(define (choose-branch bit branch)
    (cond 
        ((= bit 0) (left-branch branch))
        ((= bit 1) (right-branch branch))
        (else
            (error "bad bit -- CHOOSE-BRANCH" bit)
        )
    )
)

(define (make-leaf symbol weight)
    (list 'leaf symbol weight)
)

(define (leaf? object) 
    (eq? (car object) 'leaf)
)

(define (symbol-leaf x) (cadr x))
(define (weight-leaf x) (caddr x))


(define (make-code-tree left right)
    (list 
        left
        right
        (append (symbols left) (symbols right))
        (+ (weight left) (weight right))
    )
)

(define (symbols tree)
    (if (leaf? tree)
    (list (symbol-leaf tree))
    (caddr tree))
)

(define (weight tree)
    (if 
        (leaf? tree)
        (weight-leaf tree)
        (cadddr tree)
    )
)

(define sample-tree
    (make-code-tree 
        (make-leaf 'A 4)
        (make-code-tree 
            (make-leaf 'B 2)
            (make-code-tree
                (make-leaf 'D 1)
                (make-leaf 'C 1)
            )
        )
    )
)

(define sample-tree
    (make-code-tree 
        (make-leaf 'A 4)
        (make-code-tree 
            (make-leaf 'B 2)
            (make-code-tree
                (make-leaf 'D 1)
                (make-leaf 'C 1)
            )
        )
    )
)


(define (successive-merge sorted-leaf-set)
    (if (<= (length sorted-leaf-set) 1)
        sorted-leaf-set
        (let
            (
                (left (car sorted-leaf-set))
                (right (cadr sorted-leaf-set))
            )

            (let 
                (
                    (new-leaf (make-code-tree left right))
                    (rest (cddr sorted-leaf-set))
                )

                (if (null? rest) 
                    new-leaf 
                    (successive-merge 
                        (adjoin-set new-leaf rest)
                    )
                )
            )
        )
    )
)


(define (generate-huffman-tree pairs)
  (successive-merge (make-leaf-set pairs))
  )


(define (encode message tree)
  (if (null? message)
      '()
      (append 
       (encode-symbol (car message) tree)
       (encode (cdr message) tree)
       )
      )
  )

对于 n=5，就使用这样的字母表：

(define n5 (list
        (list 'A 1)
        (list 'B 2)
        (list 'C 4)
        (list 'D 8)
        (list 'E 16)
    )
)

(define huffman5 (generate-huffman-tree n5))

huffman5

对于n=5的Huffman树，编码出现最频繁的符号只需要1个二进制位，而最不频繁的需要4个二进制位。

对于n=10的Huffman树，编码出现最频繁的符号仍然只需要1个二进制位，而最不频繁的需要9个二进制位。

(define n10 (list
        (list 'A 1)
        (list 'B 2)
        (list 'C 4)
        (list 'D 8)
        (list 'E 16)
        (list 'F 32)
        (list 'G 64)
        (list 'H 128)
        (list 'I 256)
        (list 'J 512)
    )
)

(define huffman10 (generate-huffman-tree n10))

huffman10

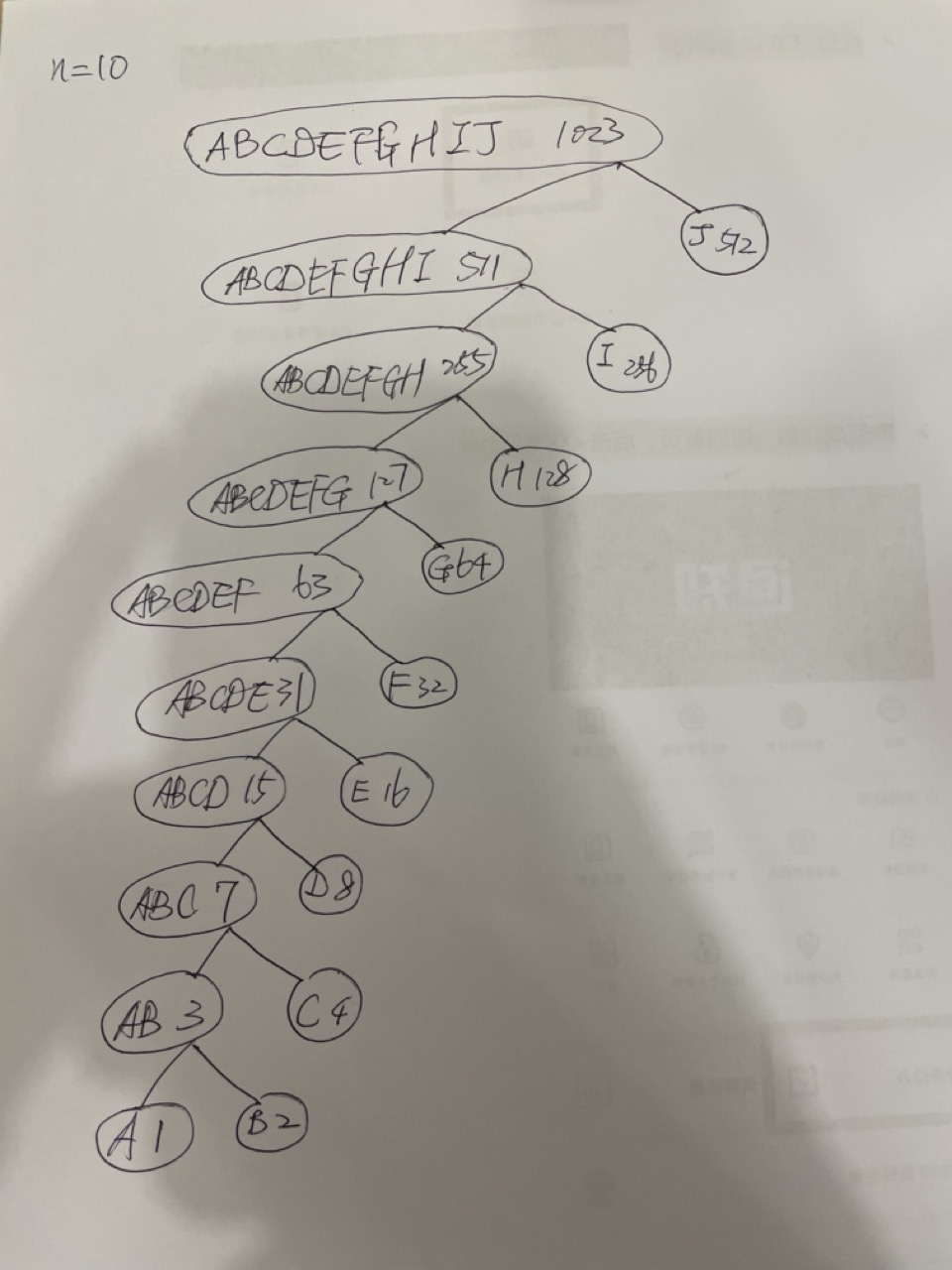
一般地说，对于这样的树，编码出现最频繁的符号只需要用1个二进制位，而最不频繁的需要n-1个二进制位。