2.37
练习 2.37 假定我们将向量 v=(vi) 表示为数的序列,将矩阵m=(mij)表示为向量(矩阵行)的序列。例如,矩阵:
用序列((1 2 3 4) (4 5 6 6) (6 7 8 9))表示。对于这种表示,我们可以用序列操作简洁地表达基本的矩阵与向量运算。这些运算(任何有关矩阵代数的书里都有描述)如下:
(dot-product v w) 返回和 ;
(matrix-*-vector m v) 返回向量 t,其中 ;
(matrix-*-matrix m n) 返回矩阵 p,其中 ;
(transpose m) 返回矩阵 n,其中 。
我们可以将点积 (dot product) 定义为:
(define (dot-product v w)
(accumulate + 0 (map * v w)))
请填充下面过程里缺失的表达式,它们计算出其他的矩阵运算结果(过程 accumulate-n 在练习 2.36 中定义)。
(define (matrix-*-vector m v)
(map <??> m))
(define (transpose mat)
(accumulate-n <??> <??> mat))
(define (matrix-*-matrix m n)
(let ((cols (transpose n)))
(map <??> m)))
首先,定义 accumulate
(define (accumulate op initial sequence)(if (null? sequence)initial(op (car sequence)(accumulate op initial (cdr sequence)))))x#<undef>
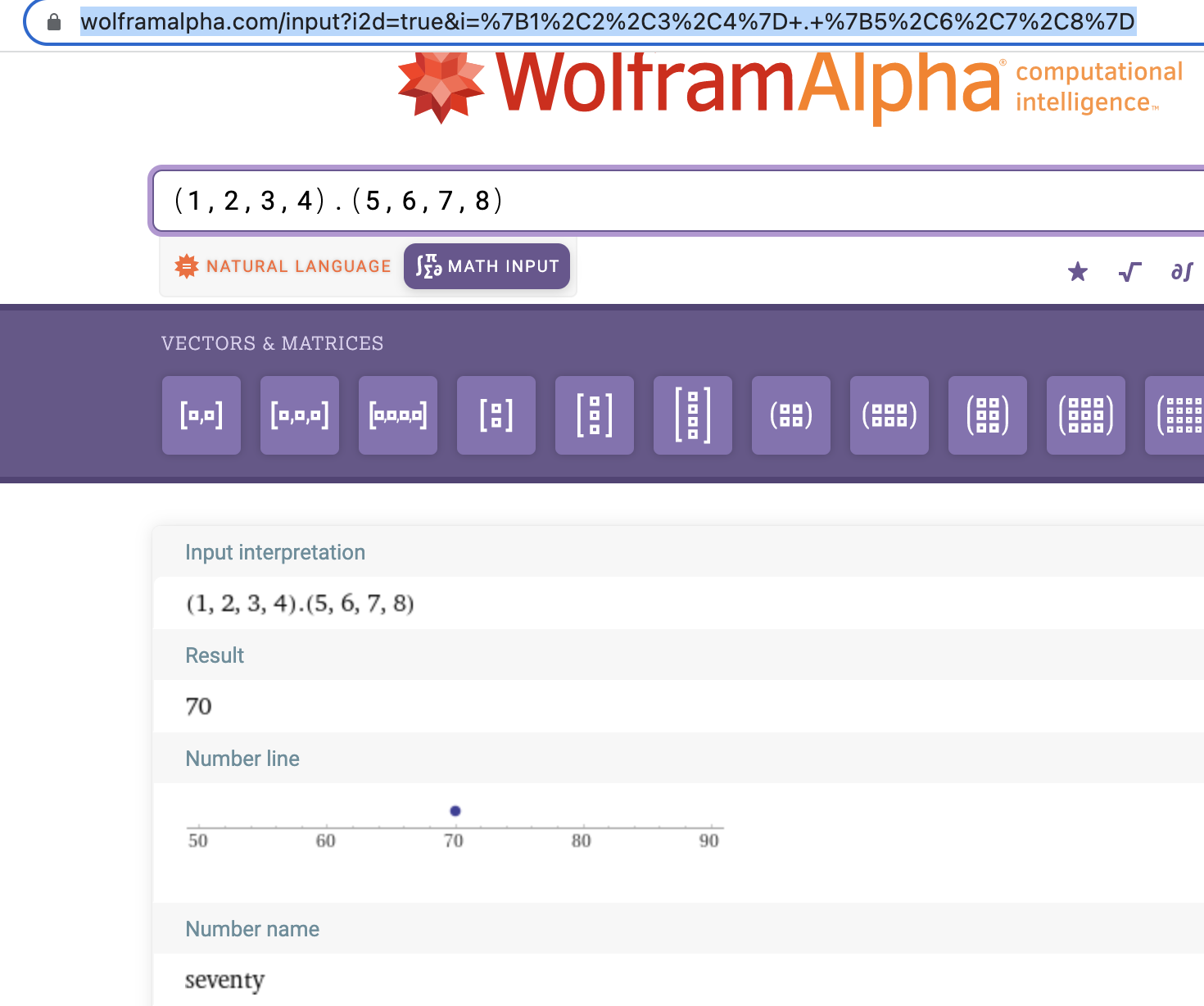
(define (dot-product v w)(accumulate + 0 (map * v w)))(dot-product (list 1 2 3 4) (list 5 6 7 8))70
对比:
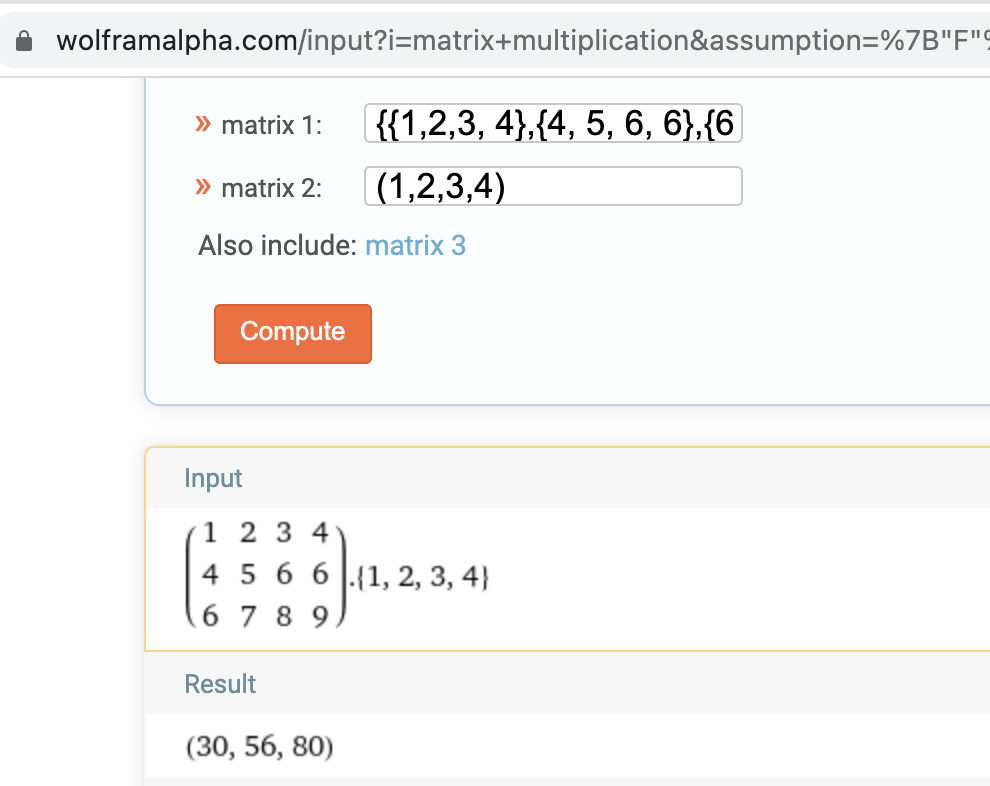
(define (matrix-*-vector m v)(map (lambda (m_i) (dot-product m_i v)) m))(define m (list (list 1 2 3 4) (list 4 5 6 6) (list 6 7 8 9)))(define v (list 1 2 3 4))(matrix-*-vector m v)(30 56 80)
对比:
然后,再定义 accumulate-n
(define (accumulate-n op init seqs)(if (null? (car seqs))'()(cons (accumulate op init (map car seqs))(accumulate-n op init (map cdr seqs)))))(define s (list (list 1 2 3) (list 4 5 6) (list 7 8 9) (list 10 11 12)))(accumulate-n + 0 s)(22 26 30)
(define (transpose mat)(accumulate-n cons '() mat))(transpose m)((1 4 6) (2 5 7) (3 6 8) (4 6 9))
(define (matrix-*-matrix m n)(let ((cols (transpose n)))(map (lambda (v) (matrix-*-vector cols v)) m)))(define n (transpose m))(matrix-*-matrix m n)((30 56 80) (56 113 161) (80 161 230))
对比:
